Minggu, 18 November 2018
Apa itu Eksponen Matematika?
Eksponen sering kita kenal dengan sebutan pangkat. Definisi eksponen adalah nilai yang menunjukkan derajat kepangkatan (berapa kali bilangan tersebut dikalikan dengan bilangan tesebut juga) Heheh aga rumit mengartikan definisinya dalam kata-kata. Bentuk an (baca: a pangkat n) disebut bentuk eksponensial atau perpangkatan. a disebut dengan bilangan pokok (basis) dan n disebut eksponennya. Jika n adalah bilangan bulat positif maka definisi dari eksponen
an = a x a x a x ….. x a (a sejumlah n faktor)
contoh : 34 = 3 x 3 x 3 x 3 = 81
dalam eksponen, bilangan pangkat tidak selamanya selalu bernilai bulat positif tetapi dapat juga bernilai nol, negatif, dan pecahan.
Eksponen (pangkat) nol
Jika a ≠ 0 maka a0 = 1
contoh
20 =1
30 =1
1283840 =1
x0 =1
contoh
20 =1
30 =1
1283840 =1
x0 =1
Eksponen (pangkat) negatif dan pecahan
Jika m dan n adalah bilangan bulat positif maka
(i) a-n = 1/an
contoh
2-3 = 1/23 = 1/8
(ii) a1/n = n√a
contoh
21/2 = √2
21/3 = 3√2
Setelah sobat hitung berkenalan dengan eksponen, kita lanjut ke sifat-sifatnya.
(i) a-n = 1/an
contoh
2-3 = 1/23 = 1/8
(ii) a1/n = n√a
contoh
21/2 = √2
21/3 = 3√2
Setelah sobat hitung berkenalan dengan eksponen, kita lanjut ke sifat-sifatnya.
Sifat-sifat Eksponen
Dari definisi eksponen di atas dapat datarik kesimpulan tentang karakteristik dan sifat-sifat dari eksponen.
- am . an = am+n
Jika sobat punya bilangan dasar sama dengan pangkat berbeda maka hasil perkaliannya adalah bilangan dasar dengan pangkat hasil penjumlahan pangkat masing-masing bilangan.
Contoh:
x4 . x6 = x(4+6) = x10
74 . 7-2 = 7(4-2) = 72 - am/an = am-n
Kebalikan dari sift pertama kalau bilangan dasar yang sama membagi salah satu, maka pangkatnya dikurangi
Contoh:
x1/2 : x1/4 = x(1/2-1/4) = x1/4 - (am)n = amn
Suatu bilangan berpangkat jika dipangkatkan lagi maka pangkat akhirnya adalah perkalian pangkatnya
Contoh:
(32)3 = 32.3 = 36 - (am.bn)p = amp. bnp
Contoh:
(x2.y3)2 = x2.2 . y3.2 = x4.y6 - (am/an)p = amp/anp
Contoh
(23/24)3 = 23.3/24.3 = 29/212
Fungsi Eksponen dan Grafiknya
fungsi eksponene merupakan pemetaan bilangan real x ke ax dengan a > 0 dan a ≠ 1. Jika a > dan a ≠ 1, x ∈ R maka f:(x) = ax disebut sebagai fungsi eksponen.
Fungsi eksponen y = f(x) = ax; a> 0 dan a ≠ 1 mempunyai sifat-sifat
Fungsi eksponen y = f(x) = ax; a> 0 dan a ≠ 1 mempunyai sifat-sifat
- Kurva terletak di atas sumbu x (definit positif)
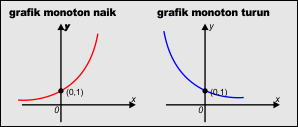
- memotong sumbu y di titik (0,1)
- mempunyai asimto datar y = 0 (sumbu x)
- grafik monoton naik untuk x > 1
- grafik berbentuk monoton turun untuk 0<x<1
Contoh Soal:
Jika f(x) = 2x+1 tentukan nilai dari f(3) dan f(-3)
f(3) = 23+1 = 24 = 16
f(-3) = 2-3+1 = 2-2 = 1/4 = 0,25
f(3) = 23+1 = 24 = 16
f(-3) = 2-3+1 = 2-2 = 1/4 = 0,25
Persamaan Fungsi Eksponen
ada beberapa bentuk persamaan eksponen diantaranya adalah
(i) jika af(x) = ap maka f(x) = p
(ii) jika af(x) = ag(x) maka f(x) = g(x)
(i) jika af(x) = ap maka f(x) = p
(ii) jika af(x) = ag(x) maka f(x) = g(x)
Contoh Soal
tentukan nilai dari x agar 32x-3 = 0
jawab
32x-3 = 0
32x =31
2x = 1 maka x = 1/2
tentukan nilai dari x agar 32x-3 = 0
jawab
32x-3 = 0
32x =31
2x = 1 maka x = 1/2
tentukan nilai x dari persamaan 35x-1 – 27x+3 = 0
jawab
35x-1 – 27x+3 = 0
35x-1 = (33)x+3
35x-1 = 33x+9
5x-1 = 3x + 9
2x = 10
x = 5
jawab
35x-1 – 27x+3 = 0
35x-1 = (33)x+3
35x-1 = 33x+9
5x-1 = 3x + 9
2x = 10
x = 5
cari himpunan penyelesaian dari persamaan eksponen 32x+2 + 8.3x -1 = 0
jawab
32x+2 + 8.3x -1 = 0 untuk memudahkan mengerjakannya sobat bisa memisalkan 3x = a
32x+2 + 8.3x -1 = 0
32x 32+ 8.3x -1 = 0
(3x)2 32+ 8.3x -1 = 0
9a2 + 8a -1 = 0 kita faktorkan persamaan kuadrat tersebut
(9a-1)(a+1) = 0
9a-1 = 0
9a = 1
a = 1/9
atau
a + 1 = 0
a = -1
kembali ke permisalan awal 3x = a
3x = 1/9 maka x = -2
3x = -1 (tidak memenuhi) jadi nilai x yang memenuhi adalah -2
jawab
32x+2 + 8.3x -1 = 0 untuk memudahkan mengerjakannya sobat bisa memisalkan 3x = a
32x+2 + 8.3x -1 = 0
32x 32+ 8.3x -1 = 0
(3x)2 32+ 8.3x -1 = 0
9a2 + 8a -1 = 0 kita faktorkan persamaan kuadrat tersebut
(9a-1)(a+1) = 0
9a-1 = 0
9a = 1
a = 1/9
atau
a + 1 = 0
a = -1
kembali ke permisalan awal 3x = a
3x = 1/9 maka x = -2
3x = -1 (tidak memenuhi) jadi nilai x yang memenuhi adalah -2
