Nilai mutlak atau disebut juga nilai absolut menggambarkan jarak nomor di baris nomor dari 0 tanpa mempertimbangkan jumlah dari arah mana nol terletak. Nilai absolut dari nomor tidak pernah negatif.

Misalnya Nilai absolut dari 5 adalah 5 (jarak dari 0 yaitu 5 unit), Nilai mutlak dari -5 adalah 5 (jarak dari 0: 5 unit). Lihat gambar:

Nilai mutlak dari 2 + -7 adalah 5 (jumlah jarak dari 0: 5 unit). Lihat gambar:

Nilai mutlak dari 0 = 0, kita tidak mengatakan bahwa nilai absolut tersebut dari angka positif.Nol tidak negatif atau positif. Lihat gambar:

Mari kita lanjutkan belajar nilai mutlak dengan contohnya di bawah ini.

Simbol untuk nilai mutlak adalah dua garis lurus, sekitarnya jumlah atau ekspresi yang mengindikasikan nilai mutlak.

| 6 | = 6 berarti nilai absolut dari 6 adalah 6.

| -6 | = 6 berarti nilai absolut dari negative6 adalah 6.

| -2 – x | berarti nilai absolut dari negative2 dikurangi x.

– | x | berarti nilai negatif dari nilai absolut dari x.

Garis bilangan bukan hanya cara untuk menunjukkan jarak dari nol, itu juga merupakan cara yang baik untuk menunjukan grafik nilai absolut.

Coba pikirkan | x | = 2. Untuk menampilkan x pada garis bilangan, Anda harus menunjukkan setiap nomor yang nilainya mutlak adalah 2.

Sekarang pikirkan tentang | x | > 2. Untuk menampilkan x pada garis bilangan, Anda harus menunjukkan setiap nomor yang nilainya absolut lebih besar dari 2. Ketika Anda membuat grafik pada garis bilangan, sebuah titik yang terbuka menunjukkan bahwa jumlah ini bukan bagian dari grafik. Simbol > menunjukkan bahwa jumlah yang dibandingkan tidak termasuk dalam grafik.

Secara umum, Anda mendapatkan dua set nilai untuk ketidaksetaraan dengan | x | > beberapa nomor atau dengan | x | =beberapa nomor.

Sekarang coba pikirkan | x | = 2. Anda mencari nomor yang nilai mutlaknya kurang dari atau sama dengan 2. Ternyata bahwa semua bilangan real dari negative2 melalui 2 membuat ketimpangan yang benar. Ketika Anda membuat grafik pada garis bilangan, titik tertutup menunjukkan bahwa jumlah ini termasuk bagian dari grafik. Simbol = menunjukkan bahwa jumlah yang dibandingkan termasuk dalam grafik.

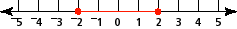
Secara umum, Anda mendapatkan satu set nilai untuk ketidaksetaraan dengan | x | < beberapa nomor atau dengan | x | = beberapa nomor. Cara mudah untuk menulis jenis-jenis kesenjangan untuk menunjukkan bahwa nilai-nilai mereka lebih kecil antara dua angka adalah:

Untuk | x | <2, negative2 <x <2

Untuk | x | = 4, negatif 4 = x = 4

Untuk | x + 6 | <25, negatif 25 <x + 6 <25

Tentu saja, dengan kurang dari ketidaksetaraan, | x | tidak akan kurang dari 0, jadi meskipun x bisa negatif, jumlah Anda membandingkannya dengan tidak bisa (atau tidak akan ada poin yang digambarkan pada baris nomor Anda).

Contoh Soal 1

Q: Selesaikanlah persamaan -3|x-4|+5 = 14

A: Cara Menyelesaikannya:

Pertama-tama kita harus mengisolasi nilai mutlak caranya adalah dengan memisahkan nilai mutlak agar berada pada satu ruas, sementara suku yang lain kita pindahkan menuju ruas yang lain.

-3|x-4|+5 = 14

-3|x-4|= 14 – 5

-3|x-4|= 9

|x-4|= 3

Pada persamaan nilai mutlak x-4 adalah “X” sehingga kita bisa menyimpulkan bahwa:

x-4 = 3 atau x-4 = -3

sehingga

x = 7 atau x = 1

maka himpunan penyelesaian dari persamaan di atas adalah {7,1}

Contoh Soal 2

Q: Tentukanlah himpunan penyelesaian dari persamaan |4 – 2/5 x|-7 = 13

A: Cara Menyelesaikannya:

|4 – 2/5 x|-7 = 13

|4 – 2/5 x|= 13 + 7

|4 – 2/5 x|= 20

maka

|4 – 2/5 x|= 20 atau |4 – 2/5 x|= -20

sehingga

– 2/5 x = 16 atau -2/5 x = -24

x = -40 atau x = 60

Maka himpunan penyelesaiannya adalah {-40,60}

Karena cukup sulit untuk menjelaskan materi Matematika dalam bentuk tulisan, maka kami mohon maaf jika penjelasannya kurang bisa dimengerti. Terima kasih telah menyimak.